재 귀(Recursion)

재귀함수의 기본적 이해

재귀함수란 함수 내에서 자기 자신을 다시 호출하는 함수를 의미한다.

  void Recursive(void) {
    System.out.println("Recursive call!");
    Recursive();  // 자신을 다시 호출한다.
  }

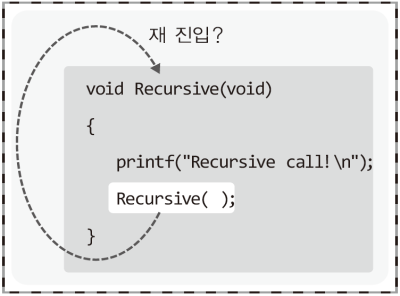
함수를 구성하는 명령문은 CPU로 이동(복사)되어서 실행이 된다. 이 명령문을 이동(복사)하는데 제한이 없다. 따라서 Recursive 함수의 중간 쯤을 실행하는 중간에 다시 Recursive 함수의 앞 부분에 위치한 명령문을 CPU로 이동시키는 것은 문제가 되지 않는다. 그래서 재귀적인 형태의 함수호출이 가능한 것이다.

재귀함수에는 ‘탈출조건’이 들어가야 한다. 그렇지 않으면 재귀함수가 한번 호출되면 계속해서 호출되기 때문이다.

팩토리얼(factorial)

재귀함수의 대표적인 예시로 팩토리얼(factorial)이 있다. 정수 $n$의 팩토리얼은 $n!$로 표시하며 이는 다음과 같다.

$n! = n \times (n-1) \times (n-2) \times (n-3) \times … \times 2 \times 1$

위 수식을 잘 보면 다음과 같이 표현 할 수 있다는 것을 알 수 있다.

$n! = n \times (n-1)!$

정수 $n$팩토리얼은 정수 $n$과 $n-1$팩토리얼의 곱으로 표현할 수 있으므로, n팩토리얼 f(n)을 수식적으로 표현하면 다음과 같다.

$f(n) = \begin{cases} n \times f(n-1) & …. \; n \geq 1 \\ 1 & …. \; n=0 \end{cases}$

팩토리얼의 식과 탈출 조건을 if~else문으로 표현하면 factorial 함수가 완성된다.

  public int Factorial(int n) {
    if(n == 0) {
      return 1;
    } else {
      return n * Factorial(n - 1);
    }
  }

재귀의 활용

피보나치 수열 : Fibonacci Sequence

피보나치 수열은 재귀적인 형태를 띠는 대표적인 수열이다. 피보나치 수열의 $n$번째 위치의 값을 반환하는 함수를 수학적으로 표현하면

$fib(n) = \begin{cases} 0 & …. \, n=1 \\ 1 & …. \, n=2 \\ fib(n-1) + fib(n-2) & …. \, otherwise \end{cases}$

이 된다. 위의 수식을 코드로 옮겨적으면 다음과 같이 정의된다.

  public int Fibo(int n) {
    if(n == 1) {
      return 0;
    } else if(n == 2) {
      return 1;
    } else {
      return Fibo(n - 1) + Fibo(n - 2);
    }
  }

이진 탐색 알고리즘의 재귀적 구현

이진 탐색 알고리즘은 두 번째 시도부터 탐색 대상을 찾을 때까지 동일한 패턴을 반복한다. 따라서 알고리즘 자체는 재귀적인 성격을 지니고 있다. 이진 탐색 알고리즘의 재귀적인 구현을 정리해보면 다음과 같다.

• 탐색 범위의 중앙에 목표 값이 저장되었는지 확인
• 저장되지 않았다면 탐색 범위를 반으로 줄여서 재탐색
• 시작위치 값이 탐색 범위의 끝보다 커지면 탈출

위의 세 가지 조건을 가지고 구현해보면 다음과 같다.

  public int BSearchRe(int arr[], int first, int last, int target) {
    int mid;

    if(first > last) return -1;  // 탐색 실패

    mid = (first + last) / 2;

    if(arr[mid] == target) {
      return mid; // 탐색된 타겟의 인덱스 값 반환
    } else if(target < arr[mid]) {
      return BSearchRe(arr, first, mid - 1, target);
    } else {
      return BSearchRe(arr, mid + 1, last, target);
    }
  }

하노이 타워 : The Tower of Hanoi

하노이 타워 문제의 이해

하노이 타워 문제는 ‘하나의 막대에 쌓여 있는 원반을 다른 하나의 원반에 그대로 옮기는 방법’에 관한 것이다.

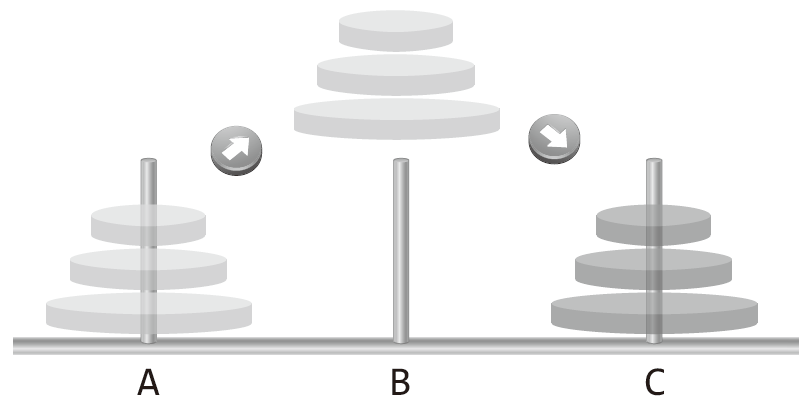
원반을 옮기는데 있어서 제약조건이 존재한다.

• 원반은 한 번에 하나씩만 옮길 수 있다. 옮기는 과정에서 작은 원반 위에 큰 원반이 올 수 없다.

원반을 옮기기 위해서는 ‘B’막대를 활용하여 ‘A’에 있는 원반들을 ‘C’로 옮겨야 한다. 원반이 3개 일 때는 비교적 해결하기가 쉽다. 원반의 개수가 늘어나도 방법은 동일하지만 같은 과정의 반복 횟수가 늘어난다.

4개의 원반을 옮기는 과정을 생각해보면, 3개의 원반을 옮기는 과정이 먼저 시행된다는 것을 알 수 있다. 이러한 반복패턴을 살펴보면 다음과 같다.

1. 작은 원반 $n-1$개를 A에서 B로 이동
2. 큰 원반 1개를 A에서 C로 이동
3. 작은 원반 $n-1$개를 B에서 C로 이동

원반 $n$개를 이동하는 문제는 원반 $n-1$개를 이동하는 문제로 나눌 수 있고, $n-1$개를 이동하는 문제는 $n-2$개를 옮기는 문제로 나눌 수 있다.

하노이 타워 문제의 해결

위에서 찾은 과정을 정리해보면 다음과 같이 구성할 수 있다.

• 작은 원반 $n-1$개(맨 아래의 원반 제외)를 A에서 B로 이동
• 큰 원반(맨 아래의 원반) 1개를 A에서 C로 이동
• 작은 원반 $n-1$개(첫 번째 과정에서 옮겨진 원반)를 B에서 C로 이동

위 조건을 가지고 코드를 작성하면 다음과 같다.

  // from에 꽂혀있는 num개의 원반을 by를 거쳐 to로 이동
  public void HanoiTowerMove(int num, char from, char by, char to) {
    if(num == 1) { // 원반 개수가 1일 때
      System.out.println("원반 1을 " + from + "에서 " + to + "로 이동"); // A에서 C로
    } else {
      HanoiTowerMove(num - 1, from, to, by); // A에서 B로
      System.out.println("원반 " + num + "을 " + from + "에서 " + to + "로 이동");
      HanoiTowerMove(num - 1, by, from, to); // B에서 C로
    }
  }