삽입 정렬 (Insertion Sort)

이 글의 목표

  • Insertion Sort에 대해 설명할 수 있다.
  • Insertion Sort 과정에 대해 설명할 수 있다.
  • Insertion Sort를 구현할 수 있다.
  • Insertion Sort의 공간복잡도와 시간복잡도를 계산할 수 있다.
  • Insertion Sort와 Selection Sort의 차이에 대해 설명할 수 있다.

Insertion Sort란?

Insertion Sort는 2번째 원소부터 시작하여 그 앞(왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입하는 정렬이다. 이것은 개선된 Selection Sort와 유사하다.

최선의 경우 O(n)이라는 엄청난 효율성을 가지고 있어, 다른 정렬 알고리즘의 일부로 사용될 만큼 좋은 알고리즘이다.

과정

  1. 2번째 위치(index)의 값을 temp에 저장한다.
  2. temp와 이전에 있는 원소들을 비교하며 삽입해 나갑니다.
  3. 처음 과정으로 돌아가 다음 위치(index)의 값을 temp에 저장하고, 반복합니다.

예시

void insertionSort(int[] arr) {
  for(int i = 1; i < arr.length - 1; i++) {
    int temp = arr[i];
    int prev = i - 1;

    while((prev >= 0) && (arr[prev] > temp)) {
      arr[prev + 1] = arr[prev];
      prev--;
    }
    arr[prev + 1] = temp;
  }
  System.out.println(Arrays.toString(arr));  
}

GIF로 이해하는 Bubble Sort

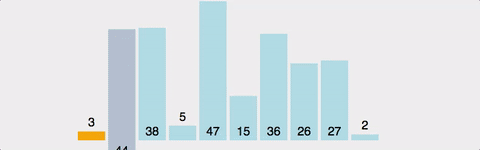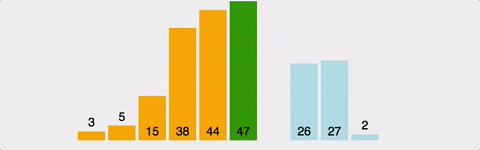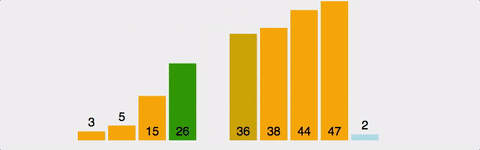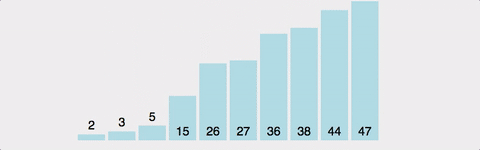
insertionsort

공간복잡도

하나의 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n)이다.

시간복잡도

  • 최선의 경우
    • 비교 횟수
      • 이동 없이 1번의 비교만 이루어진다.
      • 외부 루프 : n-1번

최선의 경우 O(n)이다.

  • 최악의 경우(입력 자료가 역순일 경우)
    • 비교 횟수
      • 외부 루프 안의 각 반복마다 i번의 비교 수행
      • 외부 루프 : n-1, n-2, …, 2, 1번 = n(n-1)/2 = O(n2)

평균과 최악의 경우 시간복잡도는 O(n2)이다.

장점

  • 알고리즘이 단순하다.
  • 대부분의 원소가 정렬되어 있는 경우, 매우 효율적이다.
  • 제자리 정렬(in-place sorting) : 정렬하려는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간이 필요하지 않다.
  • 안정 정렬(Stable Sort)이다.
  • Bubble Sort나 Selection Sort같은 O(n2) 알고리즘과 비교하여 상대적으로 빠르다.

단점

  • 평균과 최악의 시간복잡도가 O(n2)이므로, 비효율적이다.
  • Bubble Sort나 Selection Sort와 마찬가지로, 배열의 길이가 길수록 비효율적이다.

Reference