Written by
Sunwoo Han
on
on
선택 정렬(Selection Sort)
선택 정렬 (Selection Sort)
이 글의 목표
- Selection Sort에 대해 설명할 수 있다.
- Selection Sort 과정에 대해 설명할 수 있다.
- Selection Sort를 구현할 수 있다.
- Selection Sort의 공간복잡도와 시간복잡도를 계산할 수 있다.
Selection Sort란?
Selection Sort는 Bubble Sort보다도 쉽고 간단한 알고리즘이다. 해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘이다. 즉 정렬순서에 맞게 하나씩 선택해서 옮기는, 옮기면서 정렬이 되게 하는 것이다.
Insertion Sort와 헷갈릴 수 있는데, Selection Sort는 배열에서 해당 자리를 선택하고 그 자리에 오는 값을 찾는 것이라고 생각하면 된다.
과정
- 주어진 배열에서 최소값을 찾는다.
- 최소값을 맨 앞에 위차한 값과 교체(pass)한다.
- 맨 앞을 제외한 나머지 배열을 같은 방법으로 교체한다.
예시
void selectionSort(int[] arr) {
int indexMin, temp;
for(int i = 0; i < arr.length - 1; i++) {
indexMin = i;
for(int j = i + 1; j < arr.length; j++) {
if(arr[j] < arr[indexMin]) {
indexMin = j;
}
}
temp = arr[indexMin];
arr[indexMin] = arr[i];
arr[i] = temp;
}
System.out.println(Arrays.toString(arr));
}
GIF로 이해하는 Bubble Sort
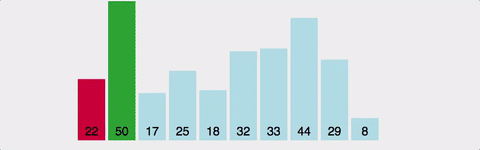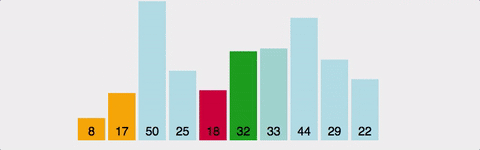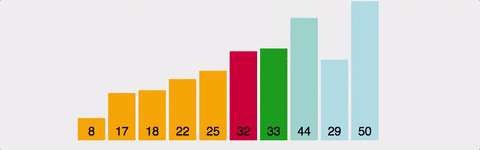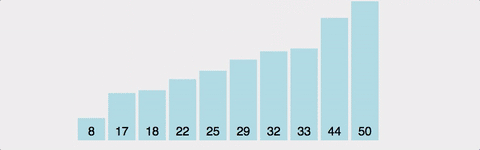
공간복잡도
하나의 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n)이다.
시간복잡도
Selection sort의 시간복잡도를 계산하면
- 비교 횟수
- 두 개의 for 루프의 실행 횟수
- 외부 루프 : (n-1)번
- 내부 루프(최솟값 찾기) : n-1, n-2, …, 2, 1번 = n(n-1)/2
따라서, 시간복잡도는 O(n2)이다.
장점
- 알고리즘이 단순하다.
- 비교 횟수는 많지만, Bubble Sort에 비해 실제 교환되는 횟수는 적기 때문에 많은 교환이 필요한 자료상태에서 비교적 효율적이다.
- 제자리 정렬(in-place sorting) : 정렬하려는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간이 필요하지 않다.
단점
- 시간복잡도가 O(n2)이므로, 비효율적이다.
- 불안정 정렬(Unstable Sort)이다.
Reference
Comments
CS 의 다른 글
-
HTTP 헤더 - 캐시와 조건부 요청 03 Jan 2022
-
HTTP 헤더 - 일반 헤더 26 Dec 2021
-
HTTP 상태코드 20 Dec 2021
-
HTTP 메서드 활용 17 Dec 2021
-
HTTP 메서드 12 Dec 2021
-
HTTP 기본 09 Dec 2021
-
URI와 웹 브라우저 요청 흐름 08 Dec 2021
-
인터넷 네트워크 06 Dec 2021
-
Single LinkedList 01 Oct 2021
-
ArrayList 24 Sep 2021
-
List Interface(리스트 인터페이스) 23 Sep 2021
-
자바 컬렉션 프레임워크 20 Sep 2021
-
면접 기초 질문 리스트 31 Aug 2021
-
인프라 기초 총정리 14 Aug 2021
-
하드웨어와 네트워크 기초 지식 03 Aug 2021
-
오버레이 네트워크(Overlay Network) 02 Aug 2021
-
이건 꼭 알고 가자! 면접 출제 빈도가 높은 질문들 19 May 2021
-
1분 자기소개 19 May 2021
-
백엔드 개발자 면접 / 학습내용 15 Feb 2021
-
너비 우선 탐색(breadth-first search, BFS) 22 Oct 2020
-
깊이 우선 탐색(depth-first search, DFS) 10 Oct 2020
-
크리티컬 섹션(Critical Section) 10 Sep 2020
-
삽입 정렬(Insertion Sort) 04 Sep 2020
-
선택 정렬(Selection Sort) 04 Sep 2020
-
거품 정렬(Bubble Sort) 04 Sep 2020
-
LRU 알고리즘 31 Aug 2020
-
Stack, Queue 29 Aug 2020
-
awk 명령어 사용법 24 Aug 2020
-
grep 명령어 사용법 23 Aug 2020
-
DNS의 이해 14 Aug 2020
-
대칭키와 공개키 10 Aug 2020
-
HTTP & HTTPS 10 Aug 2020
